Thousands of meters deep below the ocean’s surface, you’ll find an overwhelming majority of Earth’s largest underwater creatures. This isn’t a coincidence—it’s a phenomenon known as deep sea gigantism. Creatures living in the deep sea have the tendency to be larger than their counterparts living in shallower waters.

From the colossal squid, reaching a maximum length of 33 feet, to the lion’s mane jellyfish, of which the largest recorded specimen had a tentacle length of 120 feet, creatures in the deep sea reach astounding sizes simply unachievable on land. Amidst a cold, lonely environment that is scarce in resources, deep sea creatures have managed to not only thrive, but develop and grow into incredible sizes. This begs the question: How does deep sea gigantism occur?

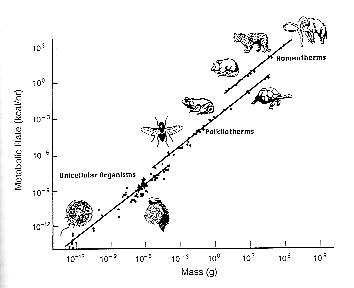
One of the foremost theories behind deep sea gigantism is Kleiber’s law. Biologist Max Kleiber hypothesized that an organism’s basal metabolic rate has a ¾ ratio to an organism’s mass. Essentially, Kleiber’s law dictates that larger animals are more efficient with their energy usage. Smaller animals would be less efficient with their energy because the energy cost per each gram of tissue would be much higher.

In contrast, having a larger body size is actually more beneficial as it uses up less energy overall. A creature with a large mass would comparatively have a slower metabolic rate than a smaller creature and thus conserve more energy. With so few resources available, energy conservation is paramount towards ensuring the survival of deep sea creatures, making size a determining factor in their ability to keep themselves alive.

Another theory behind deep sea gigantism is Bergmann’s rule, stating that the sizes of animals increase as the temperatures decrease. The underlying reason for this is that as the volume of an animal increases, its surface area increases more slowly. Since animals lose heat through their surface, a larger surface area relative to their body volume leads to faster heat loss. By minimizing the surface area to volume ratio, larger animals can better maintain body heat in low temperatures.

This rule applies to ocean animals; the ocean surface near tropics is around 30 degrees Celsius, while the ocean floor ranges anywhere from 0-3 degrees Celsius. Amid the icy depths of the deep sea, devoid of sunlight, energy is an important commodity for creatures to conserve. Bergmann’s rule is further supported by the fact that gigantism most commonly occurs in the Arctic or Antarctic seas, where even organisms living in shallow waters tend to exhibit gigantism. 

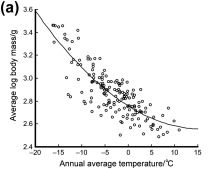
However, critics of Bergmann’s rule say that it doesn’t account for resource availability at these depths, as at colder temperatures resources are often quite scarce. As a result, it’s possible that creatures have developed their size as a result of stocking up on energy through fat stores rather than a need to lose less energy. Body mass, in fact, is more likely to experience fluctuations due to changes in food availability. Still, while Bergmann’s rule is certainly subject to its fair share of criticism, it doesn’t change the fact that, alongside Kleiber’s law, it is the best possible answer as to why deep sea gigantism exists.

Ultimately, the most likely explanation for deep sea gigantism is a combination of both Kleiber’s law and Bergmann’s rule. Larger animals are simply more well-suited to the frigid, desolate conditions of the deep sea. Resource conservation is a top priority in such a hostile environment, meaning that a slower metabolic rate and a lower capacity for heat loss are pivotal advantages in the deep.

As our exploration of the deep sea continues to progress, there is always potential in the future for new theories to crop up. However, as it stands, Kleiber’s law and Bergmann’s rule prove to be the most satisfactory conclusions for now.